
Введение
Однажды учитель физики обратился к уважаемому профессору, заведующему кафедрой компьютерных наук с вопросом: сколько верных знаков нужно сохранять при делении одного числа на другое в ваших компьютерных программах? Естественно, в том случае, когда это не удаётся выполнить точно. Вопрос несколько удивил профессора. И с некоторым снисхождением он ответил вопросом на вопрос: А сколько знаков вам нужно? Потом, не ожидая ответа, – можно 16, можно 32, можно и в десятеричной системе счисления, пожалуйста.
В самом деле, пусть калькулятор компьютера выполняет деление 1:3 = 0,333… Сколько троек нужно сохранить в результате? Понятно, что для математика этот вопрос схоластический и он, скорее всего, ответит на него так же, как и наш профессор. А что скажет физик? Он вспомнит, что любое деление производится с измеряемыми величинами. И не последнюю роль при этом будет играть точность, с которой известны числитель и знаменатель.
И здесь мы подходим к главной задаче нашего повествования. Перед тем, как обратиться к ответу на вопрос, поставленный профессору, скажем немного об измерениях вообще и в физике в частности.
Измерения лежат в основе точных естественных наук – физики, химии и многих других. Великий Галилео Галилей, с которого началась физика, как последовательная и чётко определённая наука, в основу изучения природы положил измерение. А измерение неизбежно выполняется с некоторой точностью.
Правда, надо заметить, что даже без всяких точностей человечество создало довольно много интересных сооружений и механизмов. Как-то мой знакомый теплофизик, работавший в современной инженерной фирме в Соединённых Штатах, сказал, что ему в его расчётах вообще достаточно очень грубых оценок (иногда даже из соображений размерности) с небольшой точностью.
Чтобы подчеркнуть важность вопроса о точности измерений, приведу всем понятный пример из совершенно, казалось бы, далёкой к физике области, из экономики. Представим себе фонд, помогающий малообеспеченным, например, группе пенсионеров.
Пусть группе 300 человек отпустили 1000 гр. Сколько должны выделить каждому? Очевидно 1000/30 = 3,333… гр. Точность количества денег определяется минимальной денежной единицей, то есть 1 копейкой. Тогда, округляя по известным правилам, получим 3,33 гр.
Но вот вопрос: При «точном» делении остаётся 0,00(3)гр. Кому они достанутся? Выходит, что каждой группе не додают, целую гривну. Выигрыш небольшой, а если группа побольше, скажем, 300 000 человек? Выходит, что важно, сколько верных знаков после запятой: 16 или все-таки 2.
Теперь, когда стало понятнее, зачем вообще нужно находить погрешности измерений, было бы интересно узнать, причём здесь косвенное измерение, и вообще, что это такое? Но сначала ответим на вопрос: зачем нужна точность измерений в физике?
Вам хорошо известно, что в основе наших знаний лежат законы физики. Именно они позволили человеку создать автомобили, самолёты, поезда, ракеты, компьютеры и многое другое. Так вот, всего этого не было бы, если бы люди не умели правильно измерять разные физические величины.
Вы, наверное, знаете, что в физике есть фундаментальные постоянные. Например, скорость света, заряд электрона и другие. Точности этих постоянных уделяют особое внимание, это часто более десяти верных знаков. Зачем так много? Оказывается, даже небольшое отличие в значении этих постоянных приводит к другим законам физики. Например, показатель 2 в законе Кулона известен с точностью 2 ± 10-17. До сих пор измерения, выполненные с указанной точностью, подтверждали именно эти, хорошо известные нам ещё из школы, законы.
Поясним теперь некоторые понятия, которые позволят понять, что такое косвенное измерение и его погрешности?
Некоторые общие понятия
Прежде всего, что такое измерение вообще?
Понятие измерения обычно вводят, как операцию присвоения свойству изучаемого объекта определённого числового значения. Для выполнения этой операции необходимо иметь тело, обладающее требуемым свойством, с числовым значением, равным единице. Его называют эталоном.
Операция измерения состоит в сравнении свойства объекта наблюдения с эталонным свойством или с прибором, проградуированным в соответствующих единицах. С помощью эталона градуируют приборы для измерения долей или целого количества указанных единиц.
Свойство эталона должно быть воспроизводимым. Это значит, что результаты измерений, выполненные в любых лабораториях при одинаковых условиях, должны быть одинаковыми. Ещё одна характеристика свойства, – устойчивость, – то есть измеренные значения должны оставаться неизменными в течение времени, значительно большего, чем время измерения (кроме зависимостей величин от времени).
Непосредственное сравнение числового значения свойства с эталонным называют прямым измерением.
В процессе прямого измерения возникает вопрос, возможно ли дробление значения эталонной единицы и насколько? Другими словами, можно ли распространять значения измеряемой величины на такие, которые меньше единицы? Такую операцию считают допустимой, но до определённого предела. Числовое значение этого предела принимают за абсолютную погрешность измерения. Это такое значение доли эталонного свойства, значение которого ещё подтверждает опыт.
Более точная формулировка: абсолютная погрешность измерения Dх величины х, – это наименьшее значение, которое можно прочитать по шкале прибора. У стрелочного прибора её определяет цена деления шкалы: Сх = хмак / N, где хмак – максимально возможный отсчёт по шкале прибора, N – полное количество промежутков между соседними штрихами на шкале. У цифрового прибора цена деления – это единица последнего разряда числа, которое высвечивается на табло.
По способу установления степени достоверности различают детерминированные и случайные измерения.
Детерминированное измерение – это измерение, достоверность которого подтверждает уже один качественно выполненный опыт. При этом результат оказывается вполне достаточным. Например, измерение температуры тела человека.
Ясно, что точность не увеличится, если вместо 5 измерений ширины тетради с помощью линейки, с абсолютной погрешностью ±0,5мм, выполнить 10 или больше таких измерений. Правда, если измеряют более длинный предмет и линейку прикладывают несколько раз, то ошибка накапливается.
В лаборатории часто ограничиваются одним измерением. Мы дальше будем рассматривать именно такие одиночные измерения. При этом можно не использовать специальную математику (теорию вероятностей), которую применяют при обработке большого количества опытных данных.
Со случайными измерениями имеют дело, если делают много измерений, например, по сопротивлению спирали отбирают качественные лампочки на заводе. Отдельные измерения при этом могут отличаться больше, чем на абсолютную погрешность измерения. Иногда количество деталей очень велико, поэтому их проверяют выборочно. При обработке таких измерений как раз и нужна теория вероятностей.
Результат прямого измерения записывают в виде:
|
|
(1) |
где x – величина, о точности которой мы говорим; хо – результат одного или среднее значение нескольких измерений, δх ≡ Δх/хо – относительная погрешность измерения. Величину 1/δх называют точностью или разрешением измерения. Значение измерения лежит в диапазоне (хо - Δх, хо + Δх). Любое значение из этого диапазона одинаково достоверно (говорят: представительно).
О косвенном измерении
Теперь можно перейти к косвенному измерению. Пусть у вас имеются часы для измерения времени движения тела и миллиметровая линейка (так её называют за цену деления – помните, она определяет абсолютную погрешность измерения прибором) для измерения пройденного им пути. Требуется определить скорость тела.
Здесь, часы и линейка – приборы прямого измерения. Скорость же рассчитывают по формуле: v = Δs / Δt, где Δs – путь, пройденный телом, а Δt – время его движения. Значение скорости, в данном случае, является косвенным измерением. Можно, конечно, спросить, является ли значение скорости, полученное расчётом, результатом измерения? Так вот считают, что является.
Физики, особенно теоретики, получают множество разных формул, которые потом указанным способом проверяют на опыте. Таким образом, теоретики фактически выполняют косвенные измерения, которые подтверждают или опровергают их теории. Понятно, что для выполнения прямых измерений никакие теории не нужны. При этом очевидно, что параметр, определяемый формулой, имеет смысл, если его значение, рассчитанное по ней, превышает абсолютную погрешность соответствующего косвенного измерения.
Рассмотрим конкретный пример. Пусть погрешности прямых измерений пути и времени 1м и 1 с. Тогда простой здравый смысл говорит, что скорость 1/3 ближе к 0, чем к 1, и частное с такой точностью просто равно нулю. Тогда, при дальнейшем использовании этого вывода, при делении на скорость, мы вообще придём к абсурду.
Пусть путь известен точнее: Δs = 1,00 м. В экспериментальной физике такая запись означает, что Δs = (1,00 ± 0,01) м, то есть абсолютная погрешность измерения пути – 1 см. Пусть время Δt = 3,0 с. Тогда для нахождения скорости нужно найти частное
v = 1,00 /3,0 (м/с).
Возникает простой вопрос, аналогичный рассмотренному выше экономическому вопросу: какова точность определения такого косвенного измерения скорости. Другими словами: сколько знаков после запятой следует оставить в этом расчёте (0,3 или 0,333, или может быть другое количество знаков)? Причём проверить ответ на опыте нельзя, ведь такого прибора у вас может и не быть.
Конечно, в нашем конкретном случае, такой прибор существует, – это спидометр. Он непосредственно измеряет скорость, то есть, проградуирован в м/сек. Но, такие приборы в общем случае – редкость. И требуемую величину можно получить только расчётным путем, то есть с помощью косвенного измерения.
В известном школьном задачнике по физике Н.И. Гольдфарба приведены рекомендации по поводу округления (кстати, такие же советы дают и более серьёзные руководства, например, книга А.Н Крылова), но никаких обоснований подобным правилам нигде не приведено.
В этом месте начинаются наши загадки.
Конечно, есть способ (говорят методика) расчёта точности косвенного измерения. Сложного в этой методике ничего нет, но требуется пояснить ещё некоторые (возможно) новые для школьника понятия. Нам потребуется объяснить вам понятие «частной производной».
Немного математики
Сначала вспомним, что такое обычная производная (в школьной программе это есть). Если есть функция одной переменной, то её производной называют скорость изменения значений этой функции при изменении аргумента на очень малую величину. Простейший пример, – мгновенная скорость движения.
Но производной характеризуют не только путевую скорость. Другой пример – это изменение со временем магнитного потока в законе электромагнитной индукции Фарадея (напомним сам закон: электродвижущая сила равна с обратным знаком производной от магнитного потока по времени).
А теперь спросим: как характеризовать скорость изменения функции нескольких, например, двух переменных? Представить себе такую функцию можно как поверхность над плоскостью. Каждой точке плоскости (хо, уо) ставят в соответствие некоторую точку поверхности f(хо, уо). Функция одной переменной возникает, если провести сечение этой поверхности вертикальной плоскостью.
Если через нашу точку провести несколько плоскостей, то в каждой плоскости скорость изменения функции будет, вообще говоря, разной. Например, в плоскости
х = хо = const можно ввести обычную производную, то есть скорость изменения. Так вот, частной производной по направлению у называют обычную производную по переменной у при фиксированном значении переменной х. Пример: пусть z = f(x,у) = у3·х2, найдём частную производную от z по у. Записывают так:
 = 3у2 хо2.
= 3у2 хо2.
Теперь можно рассказать про упомянутую нами методику расчёта погрешности непрямого измерения. Делают это по формуле
|
Δu = |
(2) |
где частные производные определяют при значениях аргумента х = а, у = b, … , где а, b, … – значения отдельных измерений. Отметим, что вид формулы (2) далеко не единственный. Например, используют и такой:
|
Δu = |∂u/∂x|Δx + |∂u/∂y|Δy |
(3) |
Варианты приведенных формул отражают, если кто догадался или знает, определённый вид метрики, то есть расстояние между значениями функции в точках (а, b) и (а + Δx, b + Δу). В прямоугольной декартовой системе координат этой метрике, она называется евклидовой, соответствует расстояние:
r = .
.
Но причём здесь геометрия? Почему для физических параметров должны работать такие же формулы? В случае геометрии, евклидова метрика или, проще говоря, формула для определения расстояния подтверждается опытом. Но применение такой формулы для не связанных с геометрией физических параметров совсем не очевидно. То есть применение формул (2) и (3) для физических величин требует обоснования. Оставляя пока в стороне этот непростой вопрос, рассмотрим конкретный пример расчёта погрешности, например, по формуле (3).
Найдём абсолютную погрешность измерения ускорения силы тяжести, которое связано с измерениями длины маятника l и периода колебаний T по известной из школы формуле:
|
g = 4p2(l/T2). |
(4) |
Из (4) видно, что для косвенного измерения g достаточно прямого измерения двух параметров l и T. Если известны абсолютные погрешности этих измерений (Δl и ΔT), то по формуле (3) имеем:
|
Δǥ = 4p2·[(1/T2)·Δl + 2(l/T3)×ΔT] = ǥ·(Δl/l + 2ΔT/T). |
(5) |
Пусть l = 1,0 м и Δl = 0,1 м, T = 2,00 с и ΔT = 0,01 с, тогда
Δǥ = 4·3,142·[(1/2,002)·0,1 + 2·(1,0/2,003)·0,01] ≈ 1,09.
Таким образом
ǥ = ǥо ± Δǥ = 9,81 ± 1,09 = 9,81(1 ± 0,11).
Но почему в расчётах мы везде ограничивались, как рекомендует Н.И. Гольдфарб, только двумя знаками после запятой?
Кроме того, для определения Δǥ необходимо, вообще говоря, знать значения выражений: 1/Т2, l/Т3 или ǥ = 4p2l/T2. Но сколько верных цифр в числовом выражении каждой из этих формул – остаётся загадкой. На эти вопросы в известной литературе ответа нет.
Как видите, вопросов много, но статья и так несколько длинновата. Кое-какие ответы оставим на другой раз? Заметим только, что здесь не всё так просто, как хотелось бы, но дорогу осилит идущий. В любом случае, желаем вам удачи в самостоятельном поиске ответов.
А.М. Пальти, кандидат технических наук, старший научный сотрудник по физике ВТСП



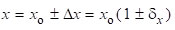







 Основатель и издатель
Основатель и издатель Copyright © 2016–2021 Научно-популярный
Copyright © 2016–2021 Научно-популярный