Иногда говорят «Если он хорошо считает, он – математик». Такая «аксиома» неправильная. Существует много определений «Кто есть математик?», «Что такое математика?». Попытаюсь тут обосновать такое своё определение: математик – это тот, кто умеет видеть Проблемы, видит Задачи вокруг себя.

Вот иду я как-то по улице и вижу объявление о том, сколько стоит вода в бутылке, рис. 1: один литр – 5 гривен, 2 литра – 8 гривен и так далее. Возникают вопросы: А какой тут закон в распределении этих чисел? А сколько стоит бутылка объёмом между 2 и 6 литрами (т.е. задача аппроксимации [1])? А сколько в случае объёма, большего 10 литров (задача экстраполяции [2], прогноза)?

Так видит математик окружающую среду: как множество интересных задач.

Давайте разберёмся в этой задачке, побудем математиками.

1. Визуализация найденных данных

Давайте, прежде всего, построим найденные данные на графике. Можно делать это «по точкам», как в школе, и это правильно. Но мы воспользуемся современным математическим компьютерным инструментом, программой MATLAB [3]. Компакт-диск с ним можно купить или загрузить бесплатно на месяц [4], или использовать его бесплатный упрощённый аналог Octave. Автор использовал MATLAB; вот как выглядит построение графика в его командном окне

>> %Построение графика:
>> Volume=[1 2 6 10]; Price=[5 8 14 17]; %Вводим в память два вектора, объём и цену
>> plot(Volume, Price,   'rp:') %Собственно, график «по точкам»
>> xlabel('Объем бутылки'),     ylabel('Цена') %Подписываем оси
>> axis([0 12, 0 18]) % размеры окна» по OX и OY
>> % Заглавие графика
>> title('Данные о стоимости бутылки воды')

и результат построения, рис. 2б.

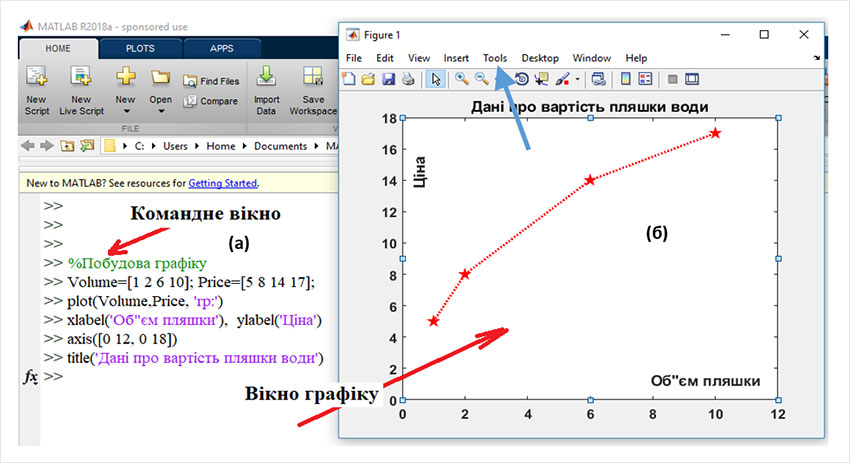
Комментарий. Временно отклонимся от данной темы для некоторых пояснений относительно нашего инструмента MATLAB. В приведенном тексте после знака процента % идёт комментарий – пояснения для человека, на которые компьютер не обращает внимания. Так мы объясняем читателю наши действия. А обозначение «>>» – это приглашение вводить команду именно в этом месте Командного Окна.

Во второй строке Командного Окна мы вводим наши числовые данные – вместимость бутылок Volume и соответствующую цену Price. Тут нужно добавить кое-что философское! А именно: главной философией MATLAB есть то, что он оперирует не только с отдельными числами, как начинают почти все другие языки программирования наивысшего уровня, а прямоугольными таблицами данных, которые называются матрицами. Собственно, данные Volume и Price – матрицы из одной строки и четырёх столбцов. Такой частный случай матрицы называют также вектором. Поэтому программа MATLAB так и называется, MATrіx LABoratory. И, продолжая эту философию, любые действия можно выполнять непосредственно с матрицами. Например:

>> Root=sqrt(Volume)   % вычисляем квадратный корень
>> SIN=sin(Volume*pi/180)   %вычисляем синус 1, 2, 6 и 10 градусов

Теперь Root и SIN – такие же числовые векторы. Только отдельные операции над матрицами выглядят немного странно, используют точку дополнительно к знаку операции:

>> Multiplication=Price .* Volume    %умножение соответствующих элементов
>> QUADRAT=Price .^ 2    % такое же умножение на себя, т.е. возведение в квадрат

Это для того, чтобы «обычные» операции сохранить для традиционных матричных действий. А приведенные «операции с точкой» обозначают действия с соответствующими членами первого и второго аргументов. Подробности в [3]. Этих объяснений пока что достаточно, идём дальше.

2. Анализируем график

Видим, что наша пока что неизвестная функция,

с помощью которой собственник вычислял цены, является монотонной. Это естественно – чем больше продукта, тем выше цена. Логично также принять, что кривая проходит через точку (0,0), т.е. для Volume=0 имеем и F(0)=0. В дальнейшем эту точку добавим к векторам Volume и Price.

С другой стороны, эта функция F(х) не является линейной y=ax+b, т.е. вдвое больший объём стоит меньше, чем удвоенная цена. Это справедливо, многие предприниматели уменьшают цены за опт. И всё-таки: какая тут функция у=F(х) использована?

Парабола y=ax²+bx+c? Нет. Парабола, как увидим далее, на рис. 6, пойдёт вниз и не будет возрастающей. Если же она направлена вверх, то она вогнута, что также не соответствует этим экспериментальным точкам. Что мы там ещё учили – y=sin(x)? Не подойдёт, т.к. в ней после определённого возрастания идёт убывание, т.е. зависимость не является монотонной.

Что там было в голове хозяина – нельзя сказать точно. Можно только гадать, допустить определённую гипотезу и искать, с какой точностью она выполняется. Точно так же «гадают» учёные относительно тех или иных зависимостей, полученных экспериментально. Примеры известны: Галилео Галилей сбрасывал разные вещи с Пизанской башни и измерял их путь за определённое время; Иоганн Кеплер на основании измерений Тихо Браге открыл законы вращения планет. Всем им и многим другим исследователям пришлось по результатам измерений искать общий закон, порядок. Потому и задача эта называется «поиск экспериментального уравнения».

3. Ищем среди многочленов,

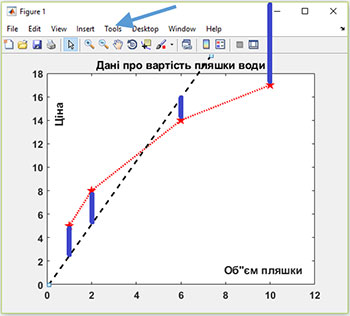
которыми, в частности, являются уже упомянутые и линейная функция, и квадратичная. Сопоставим график рис. 2б или такой же на рис. 3 с произвольной прямой, например, – штриховой на рис. 3. Понятно, что таких прямых можно провести на плоскости бесконечное количество. Какая из них будет наилучшей? Интуиция подсказывает, что этот термин «наилучшая» следует определить таким образом, чтобы она была самой близкой ко всем нашим экспериментальным точкам.

4. «Наилучшая прямая»

Очевидно, лучшая, самая близкая прямая линия не будет проходить по одну сторону от точек, а «как-то» между ними. Рис. 3 подсказывает, что следует минимизировать сумму расстояний от прямой до точек. Или – сумму квадратов расстояний…

Поздравляем! Вы только что сделали открытие, которое на 220 лет раньше сделал выдающийся немецкий математик Карл Фридрих Гаусс [5]! Остаётся только формализовать такое понятие близости, например, как минимум величины, которую называют невязкой:

Здесь y( x_i ) – значения аналитически заданной функции, которая исследуется, в точках x_i для всех i = 1,2,3,4, т.е. y_i = ax_i + b в данном случае, а y_i*– соответствующие эмпирические значения для x_i. Четыре слагаемые выбраны только потому, что у нас 4 числа в векторах. А для произвольного случая m эмпирических значений следует то же самое записать с помощью греческой буквы сигма Σ:

.

Таким образом, невязка, близость, становится зависимой от коэффициентов уравнения a и b, которые и следует отыскать. Математически строго доказано, что поиск таких коэффициентов многочлена даёт ответ всегда, и к тому же однозначный! Каким бы ни было количество экспериментальных точек m>2!

Ещё важный вопрос: обязана ли функция F(х) проходить точно через точки? Нет, не обязана, т.к. точки являются результатом измерений, в них обязательно есть какая-то погрешность, или, как в данном случае, округление цены. Метод минимизации (2) является поиском компромисса между нужной точностью и неминуемыми погрешностями.

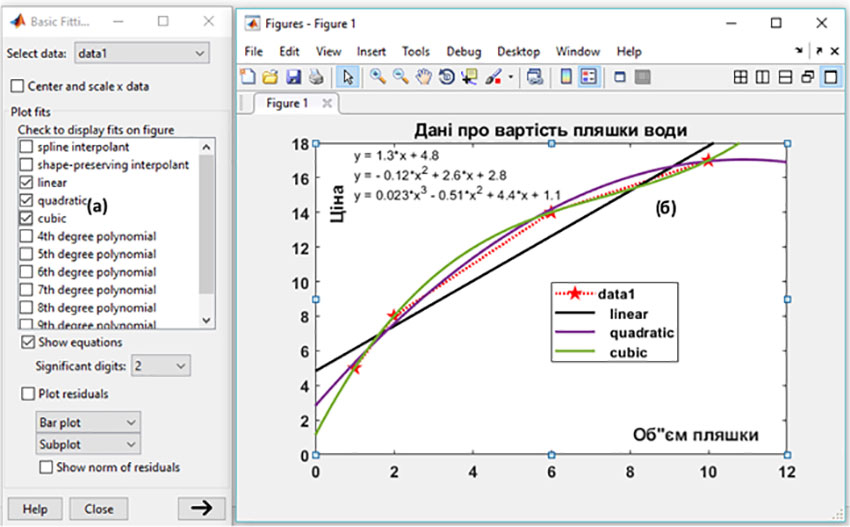
Неудивительно, что такой метод реализован и в лаборатории MATLAB. Этот метод следует искать в меню инструментов Tools, обозначенном толстой стрелкой на рис. 2 и 3. Нажимаем, видим внизу инструмент Basic Fitting (подгонка) и запускаем его. Возле нашего графического окна появляется ещё одно окно, обозначенное как (а) на рис. 4. Здесь предлагается выбрать какое-то из уравнений – linear, quadratic или cubic. Отмечаем чек-бокс – сразу видим ближайшую кривую соответствующего сорта и её уравнение с найденными коэффициентами. Делаем выводы: прямая – достаточно далеко от эксперимента. Квадратичная и кубическая кривые, хотя мы их «согнули» близко к экспериментальным точкам, всё равно справа от последней точки освобождаются и несутся вверх… Таким образом, никакая из выбранных кривых не подходит! Расчёты показывают, что наилучшая из прямых даёт, тем не менее, невязку N=4.17, а наилучшая из парабол даёт N=0.32. Хотя последний результат точнее, парабола, как уже сказано, не подходит.

5. Эврика!

Так говорил античный философ Архимед, когда его, наконец, посещала хорошая идея. Автора данной заметки также посетила идея: искать зависимость в виде квадратного корня

Проверим ее!

Но вот проблема: в MATLAB такое уравнение не предусмотрено… Нужно включать мозги!

«Эврика» относится к нахождению коэффициентов уравнения

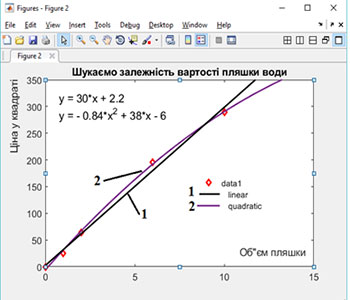
т.е. вместо экспериментальных пар (x_i,y_i*) нужно строить пары (x_i,(y_i*)²), и уже для них искать коэффициенты параболы (4). Переходим в командное окно MATLAB:  

После этого опять вызываем инструмент Basic Fitting и заказываем в нем варианты linear и quadratic. Результат представлен на рис. 5. Видим, что, действительно, обе только что найденные функции, уравнения которых записаны на рисунке, неплохо описывают наши экспериментальные точки, т.е. можно пользоваться одной из зависимостей:

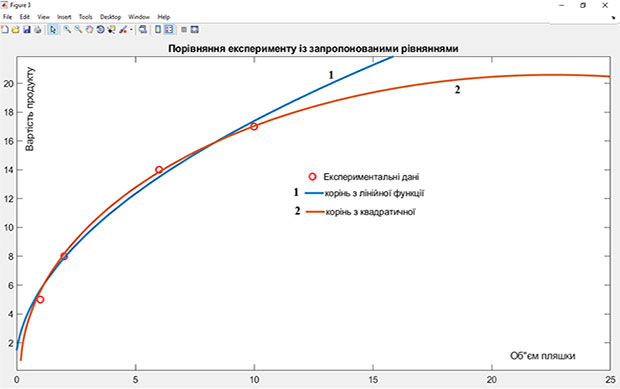
Расстояния данных кривых от экспериментальных точек равно 3 в первом случае и 5.6 во втором. Остаётся сравнить найденные уравнения с экспериментальными точками и предварительными гипотезами, которые представлены на рис. 6. Приведенные расстояния получены в MATLAB следующим образом:

Видим, что первое из уравнений (6) довольно неплохо приближает наши экспериментальные точки. Вторая кривая при условии Price > 25 начинает убывать – это не соответствует логике. Именно первое из (6) возьмём за окончательное решение поставленного вначале вопроса. Не важно, что кривая с найденным уравнением (3) или (5) не проходит строго через экспериментальные точки! Мы учитываем этим самым возможность округления «экспериментальных» данных.

Остаётся ответить на вопросы об аппроксимации (нахождение значений между известными точками), например, для Volume=3 и прогноза (за пределами известного), например, Volume=15. Вычисляем в MATLAB:

>> Volume=[3   15]; % Напоминаем: MATLAB вычисляет сразу для всех значений матрицы!
>> Price=sqrt(30*Volume+2.2)
Price =   9.6021     21.2650

Т.е. цена будет приблизительно (а точнее вряд ли нужно) 9 грн. 60 коп. за три литра, 21 грн. 27 коп. за пятнадцать. «Уличное исследование» закончено!

В заключительном разделе подытожьте то, что узнали.

Вопросы для любознательных

1. Что такое «линейная» функция? Проверьте себя, [6].
2. Что такое «многочлен»? Какой общий вид он имеет? Сколько в нём коэффициентов? А в линейном случае? (Не знаете – ищите ответ в учебнике или в Википедии).
3. В чём состоит метод наименьших квадратов, МНК? Как он определяет расстояние между экспериментальными точками и теоретической кривой? Можете ли предложить другое определение такого расстояния? Ваше мнение: можно ли ещё где-нибудь использовать такое определение?

4. На другом объявлении автор увидел такие цены 25, 2.50, 6.25, 7.50, 12.50 и 23.75 грн. за, соответственно, 1, 2, 5, 6, 10 и 19 литров. Исследуйте, какому закону подчиняются эти цены. Сколько будет стоить 3 литра? 25 литров? (Подсказка: эта задача намного проще рассмотренной!)
5. Вам понравился MATLAB – среда для математических исследований? Целесообразно ли использовать его в школьной математике?

Литература:

1. Что такое интерполяция.
2. Что такое экстраполяция.
3. Азарсков В.М., Гаєв Є.О. Сучасне програмування, две книжки. К.: НАУ, 2014 та 2017.
4. Здесь можно получить MATLAB бесплатно на 1 мес.
5. О методе наименьших квадратов.
6. Пояснение: «Что такое линейность»?

Е.А. Гаев, профессор Национального авиационного университета, г. Киев