Вступление

Изучая в школе математику и физику, учащиеся время от времени «натыкаются» на понятия «средних величин». Систематическое изучение средних величин в школьном курсе математики не проводится. Они используются лишь для формулировки некоторых задач на доказательство неравенств [1,2]. В то же время эта тема содержит в себе ряд занимательных и поучительных фактов, которые могут быть компактно изложены в рамках элементарной математики. Представляется, что такое изложение может продемонстрировать школьнику хороший пример введения математиками абстрактных понятий, их развития и применения на практике. Отметим попутно, что интерес к изучению средних величин проявляли многие отнюдь не средние учёные — от Пифагора и Аристотеля до О.-Л. Коши и А. Н. Колмогорова. Начало применению средних величин в количественном анализе общественных явлений положено выдающимся бельгийским учёным XIX века Адольфом Кетле.

Часть 1. Меж двух огней

Средняя арифметическая — любимица миллионов

Впервые о «средних» мы узнаём в детстве. Середина реки, среда (середина недели — если считать по-библейски, от воскресенья до субботы) и т.п. Во всех этих случаях интуитивно под серединой понимается точка в пространстве или во времени, равноудалённая от двух других точек, представляющих начало и конец чего-либо.

Что является математической моделью такого рода средних величин? Их интуитивному введению соответствуют постановка и решение следующей математической задачи. Имеется пара чисел a и b (b>a). Требуется найти третье число c, «равноудалённое» от a и b, т.е. такое, при котором c—a = b—c.

Историки науки утверждают, что именно так вводится понятие средней величины в трудах великого древнегреческого учёного Аристотеля (IV век до н.э.). Ясно, что решением этой задачи является .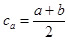

Это — знакомая по школьному курсу математики средняя арифметическая двух чисел a и b. Правда, в школе эта величина вводится формально, «по определению» — «средней арифметической двух чисел называется полусумма этих чисел» — без разъяснения «физического смысла».

Средняя арифметическая и с понятийной, и с математической точек зрения является настолько естественной, что у школьника создаётся впечатление, будто другого представления о средней величине и быть не может. И что «арифметическая» — ненужный словесный довесок.

Средняя геометрическая — любимица Галилея

Первый удар по, казалось бы, «единственной и неповторимой» средней арифметической наносит геометрия.

Высота h прямоугольного треугольника, опущенная из вершины прямого угла, больше меньшего (h_a) и меньше большего (h_b) из отрезков, на которые делит гипотенузу основание этой высоты. Формула для вычисления высоты имеет вид .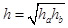

«Под впечатлением» от этой формулы величина 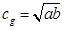названа средней геометрической чисел a и b (в отличие от средней арифметической, средняя геометрическая вводится только для положительных чисел).

Оказывается, средняя геометрическая имеет и негеометрическую интерпретацию. Если (как показано в предыдущем пункте) средняя арифметическая обеспечивает равенство отклонений, то к средней геометрической приводит равенство отношений.

Зададимся целью найти число c_g, которое относится к a (меньшему из двух чисел) так же, как b (большее из чисел) относится к c_g. Соответствующее уравнение (относительно ) имеет вид: . Его решением и является средняя геометрическая чисел a и b.

Какая же из двух упомянутых средних «более средняя» — арифметическая или геометрическая? Иными словами, какую из них следует использовать на практике?

Это зависит от целей, для которых используется средняя. В большинстве практических случаев более подходящей является первая модель, а значит средняя арифметическая является «более средней». Но не всегда!

В 1627 году имел место документально зафиксированный спор между самим Галилеем и неким монахом Ноццолино. Предмет спора заключался в следующем: «если лошадь оценена двумя оценщиками в 10 и 1000 единиц, то какую среднюю следует предпочесть в качестве величины, представляющей её действительную цену?

Среднюю арифметическую, как считал Ноццолино или среднюю геометрическую, которую предпочитал Галилей?» [3]. Много позже (в XIX веке) знаменитый математик и астроном Зайдель разрешил этот спор, доказав на основании так называемого психофизического закона Вебера-Фехнера, что «в случае, если оценка основывается исключительно на наших восприятиях, правильно применять среднюю геометрическую, а не среднюю арифметическую» [3]. То есть Галилей и тут не ошибся!

В поисках гармонии

О существовании ещё двух видов средних — средней квадратической и средней гармонической — школьники узнают при решении всё тех же задач на доказательство неравенств. Эти средние вводятся в рассмотрение формально.

Первая из них вычисляется по формуле , и активно применяется в общей [4] и математической [5] статистике. А вот вторая имеет ряд интересных содержательных интерпретаций, одна из которых приводится ниже.

Определение: средней гармонической двух чисел a и b, таких, что a≠0, b≠0 и , называется третье число c_h, вычисляемое по формуле: .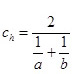

Рассмотрим задачу определения средней скорости движения автомобиля на пути от пункта А до пункта В и обратно, если путь от пункта А до пункта B он ехал со скоростью v₁, а обратный путь от B до A — со скоростью v₂. Вспоминаем из начального курса физики, что средняя скорость — это весь путь делённый на всё время пути.

Обозначим расстояние между пунктами через s. Тогда средняя скорость вычисляется по формуле . Так вот что такое средняя скорость — это и есть средняя гармоническая скоростей движений «туда» и «обратно».

Интересно, что все упомянутые средние оказываются «одного поля ягодами»! Для положительных чисел и введём в рассмотрение понятие средней s-го порядка (средневзвешенной s-й степени): .

Ясно, что M₁(a,b) – средняя арифметическая чисел a и b, M₂(a,b) – средняя квадратическая, M_-1(a,b) – средняя гармоническая. Но самое интересное, что M₀(a,b) – это средняя геометрическая чисел a и b!

Правда, здесь подразумевается применение операции предельного перехода, т.е. . «Голыми руками» такой предел «не берётся», т.к. имеет место неопределённость вида . Однако, она легко преобразуется в неопределённость вида 1^∞, которая устраняется с помощью всемогущего правила Лопиталя.

Только для «крутых», т.е. студентов-первокурсников! Делается это следующим образом: . Но ,  . Это уже неопределённость типа 0/0, а раз так — «выкатываем» правило Лопиталя [6].

Последний предел равен отношению пределов производных, т.е. 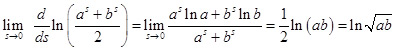. Таким образом, .

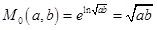Оказывается, что параметр s выстраивает средние в определённом порядке. Имеет место замечательная лемма Йенсена, а именно: M_s как функция от s при a=b постоянна, а при a₁≠a₂ строго монотонно возрастает, т.е. при s₁<s₂

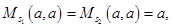
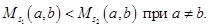
Доказательство этой леммы относительно несложно. Те, кто хочет с ним ознакомиться, могут обратиться, например, к «Выпуклым множествам» К. Лейхтвейса [7]. Из леммы Йенсена непосредственно вытекает справедливость популярных неравенств между средней арифметической, геометрической, квадратической и т.п. [1,2].

Ещё один генератор средних величин

Вернёмся к задаче о средней гармонической. Обратим внимание на то, что если бы автомобиль ехал весь свой путь (туда и обратно) со средней гармонической скоростью 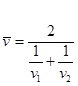, то затратил бы на прохождение пути то же самое время. В самом деле, .

Размышления над установленным свойством средней гармонической приводит к полезному понятию «численного соответствия».

Рассмотрим функцию двух переменных z=f(x₁, x₂). Число c называется численным соответствием чисел x₁, x₂ по отношению к функции f, если f(c, c) = f(x₁, x₂) .

Интуитивно числовое соответствие не противоречит понятию средней величины. Фактически же, если функция f не является слишком «экзотической», то имеет место неравенство min(x₁, x₂) ≤ c ≤ max(x₁, x₂), т.е. c является средней для чисел x₁, x₂.

Покажем, как с помощью численного соответствия можно построить уже известные нам средние величины.

1. Пусть f(x₁,x₂)=x₁+x₂. Найдём численное соответствие для данной функции. Для этого достаточно решить уравнение, вытекающие из определения числового соответствия: f(c,c)=c+c=x₁+x₂. Решив этого уравнение, находим: . Таким образом, среднее арифметическое является численным соответствием суммы двух чисел.

2. Пусть f(x₁,x₂)=x₁·x₂. Для численного соответствия составляем уравнение: f(c,c)=c·c=x₁·x₂, откуда . Таким образом, среднее геометрическое является числовым соответствием произведения двух чисел.

3. Точно также устанавливается, что средняя гармоническая является численным соответствием функции , а средняя квадратическая — числовым соответствием функции f(x₁,x₂)=x₁²+x₂².

Раз уж мы разрекламировали возможность генерирования средних величин с помощью принципа численного соответствия, то почему бы нам, действуя по аналогии с приведенными примерами, не попробовать «соорудить» что-нибудь новенькое в этом жанре?

Рассмотрим, например, функцию . Для численного соответствия получим уравнение: , откуда . Вот вам и новая средняя — осталось только придумать для неё название!

Заключение

Подведём некоторые итоги. Мы теперь знаем, что средняя величина двух чисел — это что-то «промежуточное» между этими числами, причём совсем не обязательно, чтобы это было среднее арифметическое. При построении средних величин можно использовать как формальные, так и некоторые содержательные соображения, например:

• «балансировки», когда среднее должно «сбалансировано» отличаться от «осредняемых» чисел;
• «численного соответствия», когда подстановка средней в некоторую формулу в качестве значений каждой из переменных приводит к тому же значению, что и подстановка «осредняемых» величин, т.е. .

Различия в понимании того, что такое «сбалансированность», а так же возможность варьирования функции f, являются теми развилками, отправляясь от которых можно строить различные формулы для получения средних величин.

Теперь — стоп! Дальше — для читателей-героев, дочитавших до этого места. У таких подвижников вполне может возникнуть естественный вопрос: а как быть со средними не двух величин, а большего их количества? Ведь тут никакие пропорции не помогут. Но математики с этим вопросом все-таки разобрались! О том, что у них получилось — читайте во второй части статьи, которая будет опубликована в следующем номере нашего журнала.

Литература

1. И. Х. Сивашинский. Неравенства в задачах. — М.: «Наука», 1967. — 302 с.
2. И. С. Слонимский. Элементарная алгебра. Дополнительный курс. — М.: «Наука». — 1964. — с.133-136.
3. К. Джини. Средние величины. — М.: «Статистика» — 1970. — 448 c.
4. И. С. Пасхавер. Средние величины в статистике. — М.: «Статистика».– 1979. — 279 с.
5. Г. Кимбл. Как правильно пользоваться статистикой. — М.: «Финансы и статистика». — 1982. — 294 с.
6. Корн Г. А., Корн Т. М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — с. 130-131.
7. К. Лейхтвейс. Выпуклые множества. — М.: «Наука». — 1985. — с. 250-251.

Б.Г. Тучинский, средний математик, кстати — доктор философии (PhD) по специальности «прикладная математика для экономики», старший научный сотрудник Института возобновляемой энергетики НАН Украины