Епоха еллінізму подарувала світові трьох великих математиків – Евкліда, Архімеда та Аполлонія. Аполлоній був молодшим сучасником і науковим суперником Архімеда.

Праці Евкліда і Архімеда перекладені багатьма мовами, зокрема, російською, і про цих математиків написано чимало книжок і статей. Переклади ж творів Аполлонія видавалися дуже рідко, більшість перекладів були по суті замінені переказами.

Ім’я «Аполлоній» означає «присвячений Аполлону». Місто Перга, в якому народився Аполлоній, протягом багатьох століть було пов’язане з культом Аполлона. Це місто знаходилось на південному узбережжі Малої Азії, неподалік від сучасного турецького міста Бурси. На честь рідного міста вченого називають Аполлонієм Пергським.

Ще юнаком Аполлоній відбув до Александрії, найбільшого центру елліністичної культури, де вивчав математику в послідовників Евкліда. Потім переїхав до Пергама, де очолив математичну школу і працював там до кінця життя.

Пергам славився не лише як центр виготовлення зі шкіри матеріалу для письма – пергаменту, але й своєю бібліотекою, яка за кількістю зібраних книг поступалася лише Александрійській.

Головний трактат Аполлонія – «Конічні перерізи» (інша назва – «Коніка») приніс ученому світову славу і став шедевром математичної літератури всіх часів. За ступенем складності для давньогрецького читача цей трактат був приблизно таким же, як для пересічного нашого сучасника монографія з алгебраїчної топології.

Трактат складається з восьми книг і присвячений вивченню тих кривих, які ми тепер називаємо кривими другого порядку. Всього в трактаті доведено 387 теорем.

Перші чотири книги дійшли до нас грецькою мовою – мовою оригіналу, книги 5-7 збереглися лише в перекладі арабською мовою.

Восьма книга до нас не дійшла – її зміст реконструював англійський астроном і фізик Едмонд Галлей (1656-1742) за допомогою тих відомостей, що залишили коментатори праць Аполлонія, а також спираючись на зміст попередніх семи книг.

Відомо, що конічні перерізи досліджували давньогрецькі вчені ще до Аполлонія. Так, при дослідженні задачі про подвоєння куба Менехм (IV ст. до н.е.) користувався параболою і рівнобічною гіперболою.

Приблизно в той же час Аристей писав про конічні перерізи як геометричні місця точок. Його праця втрачена. Евклід написав «Начала конічних перерізів», які до нас не дійшли. Архімед теж доводив допоміжні твердження, що відносились до такого типу кривих.

Усім цим ученим була відома основна властивість кожного з конічних перерізів, яку вони називали симптомом. Однак повне і систематичне вчення про ці криві було вперше викладене саме Аполлонієм.

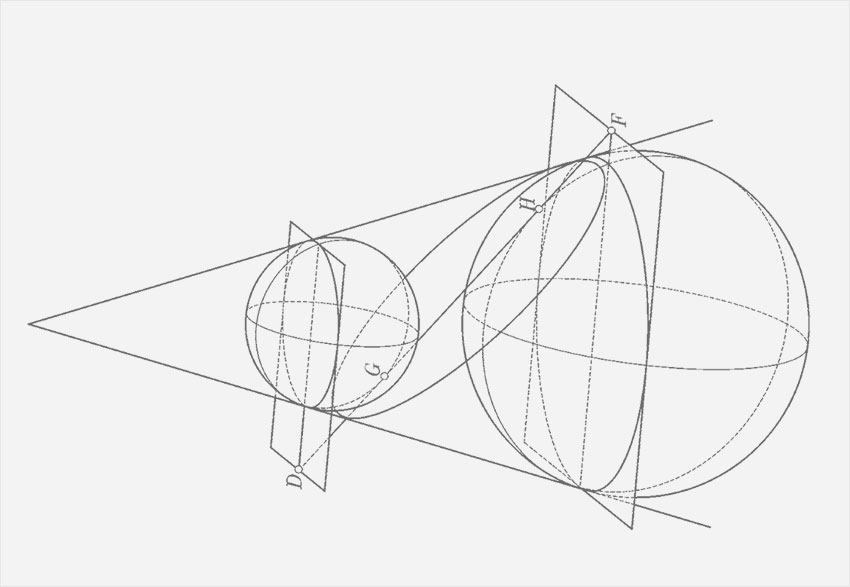
Аполлоній на відміну від своїх попередників розглядає всі три типи кривих другого порядку як плоскі перерізи одного й того ж довільного кругового конуса, порожнини якого поширюються в обидва боки від вершини. Його попередники кожен з трьох видів кривих одержували при перетині гострокутного, прямокутного і тупокутного конуса перпендикулярним до твірної перерізом.

Аполлоній отримує еліпс, гіперболу або параболу в залежності від того, чи перетинає площина лише одну порожнину конуса, обидві його порожнини або вона паралельна одній із твірних конуса.

Аполлоній уперше ввів терміни «еліпс», «гіпербола», «парабола», встановив наявність асимптот у гіперболи. Він, як і його попередники, знайшов геометричні симптоми цих кривих, тобто, сучасною мовою, їхні рівняння (у словесній формі). Звідси походить і назва самих кривих.

Для параболи площа квадрата, побудованого на ординаті у деякій її точці, дорівнює площі прямокутника D = 2px, одна сторона якого дорівнює відповідній абсцисі х, а інша – сталому відрізку 2р (подвоєному параметру параболи).

Грецьке слово «parabole» й означає «прикладення», тобто побудову прямокутника з даною основою (2р), рівновеликого до квадрата (у²).

Для еліпса площа квадрата, побудованого на ординаті у, менша площі прямокутника D. Грецьке слово «elleipsis» означає «недостача».

Для гіперболи площа квадрата (у²) більша площі прямокутника D. Звідси й грецький термін «hyperbole», що означає «надлишок»», «перевищення».

Із сучасного погляду можна сказати, що Аполлоній досліджував властивості конічних перерізів відносно прямокутної системи координат, у якій одна вісь збігалася з головним діаметром кривої, а друга – проходила через вершину кривої. При цьому вчений досліджував саме ті властивості, які залишаються незмінними (інваріантними) при допустимих перетвореннях.

Ця ідея стала зрозумілою вченим лише в XIX ст., коли була сформульована знаменита Ерлангенська програма німецького математика Фелікса Клейна.

Можна стверджувати, що навіть сучасні університетські курси аналітичної геометрії не охоплюють усіх властивостей конічних перерізів, відкритих і доведених Аполлонієм. При відсутності аналітичного методу дослідження, обсяг виконаної вченим роботи є просто велетенським.

Окрім трактату «Конічні перерізи», Аполлонію належать ще й інші праці з математики, астрономії, оптики, але майже всі вони до нас не дійшли – збереглися лише їх назви та формулювання проблем, які в них розв’язував учений. У «Загальному трактаті» він вивчав загальні твердження, які не доводяться, – аксіоми, постулати та їх відношення до реальної дійсності.

Аполлоній отримав наступне наближення числа π ≈ 62832/20000=3,1416. Він запропонував позиційну систему числення за тетрадами (степенями міріад, тобто 10000). Окремі праці вчений присвятив невпорядкованим ірраціональностям і запалювальним дзеркалам.

У двохтомному трактаті Аполлонія «Про дотики» було вміщено його знамениту задачу: «Дано три фігури на площині, кожна з яких може бути точкою, прямою або колом. Побудувати на цій площині коло, яке проходило б через дані точки (або точку) і дотикалося до даних кіл або прямих».

Вважається, що сам Аполлоній знайшов розв’язання цієї задачі, однак воно до нас не дійшло.

Лише у XVI ст. Франсуа Вієт запропонував власний варіант розв’язання цієї знаменитої задачі. Коло, яке дотикається до трьох даних кіл, отримало назву кола Аполлонія.

Саме в Аполлонія вперше зустрічається в явному вигляді вимога, щоб геометричні побудови виконувались лише за допомогою циркуля і лінійки. До нього така вимога не була загальноприйнятою в давньогрецькій математиці.

Птолемей у своєму трактаті «Альмагест» стверджує, що Аполлоній увів системи ексцентриків і епіциклів для пояснення руху планет.

Праці Аполлонія мали великий вплив на розвиток науки Нового часу – астрономії, механіки, оптики.

Його досягнення стали підґрунтям для створення аналітичної і проективної геометрії. На них спиралися не лише Галілей і Кеплер, Ферма і Декарт, але й Дезарг, Паскаль, Лейбніц, Ньютон, Ейлер, Лагранж та багато інших видатних учених.

Творчістю Аполлонія завершився найбільш блискучий період розвитку давньогрецької математики.

Іменем Аполлонія названо кратер на зворотному боці Місяця.

Література

1. Ван дер Варден Б.Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. – М., 1959.
2. Розенфельд Б.А. Аполлоний Пергский. – М., 2004.
3. Шмигевський М.В. Видатні математики. – Харків, 2004.

М.В. Шмигевський